(i) 272
Ans. Since \(\ (2)^2 = 4 \)
The digit in the unit place of the square of 272 will be 4.
(ii) 79
Ans. Since \(\ (9)^2 = 81 \)
The digit in the unit place of the square of 79 will be 1.
(iii) 400
Ans. Since \(\ (0)^2 = 0 \)
The digit in the unit place of the square of 400 will be 0.
(iv) 2637
Ans. Since \(\ (7)^2 = 49 \)
The digit in the unit place of the square of 2637 will be 9.
2. Why do the following numbers are not perfect squres?
(i) 1057
Ans. Since the digit in the unit place of 1057 is 7, so it can't be a perfect square.
(ii) 7928
Ans. Since the digit in the unit place of 7928 is 8, so it can't be a perfect square.
(iii) 222
Ans. Since the digit in the unit place of 222 is 2, so it can't be a perfect square.
(i) 400
Ans. Since the digit in the unit place of 400 is a 0 but not in the tens place alongside, so it can't be a perfect square.
[0 in not in pair starting from unit place]
4. Find the square root of the following by prime factorisation method.
(i) 1764
Solution:
\(\ 1764 = 2^2×3^2×7^2 \)
⸫ \(\ \sqrt{1764} = 2×3×7 = 42 \)
(ii) 9216
Solution:
\(\ 9216 = 2^2×2^2×2^2×2^2×2^2×3^2 \)
⸫ \(\ \sqrt{9216} = 2×2×2×2×2×3 = 96 \)
(iii) 7744
Solution:
\(\ 7744 = 2^2×2^2×2^2×11^2 \)
⸫ \(\ \sqrt{7744} = 2×2×2×11= 88 \)
(iv) 9801
Solution:
\(\ 9801 = 3^2×3^2×11^2 \)
⸫ \(\ \sqrt{9801} = 3×3×11 = 99 \)
5. Find the least number (integer) with which the following numbers are to be multiplied so that they become perfect squares.
(i) 1525
Solution:
\(\ 1525 = 5^2×6 \)
⸫ The number 1525 is to be multiplied by 6 so that it becomes a perfect square.
(ii) 1008
Solution:
\(\ 1008 = 2^2×2^2×2^2×7 \)
⸫ The number 1008 is to be multiplied by 7 so that it becomes a perfect square.
(iii) 2028
Solution:
\(\ 2028 = 2^2×3×13^2 \)
⸫ The number 2028 is to be multiplied by 3 so that it becomes a perfect square.
(iv) 768
Solution:
\(\ 768 = 2^2×2^2×2^2×2^2×2^2×3 \)
⸫ The number 768 is to be multiplied by 3 so that it becomes a perfect square.
6. With what least numbers (integers) the following numbers are to be divided so that they become perfect squares.
(i) 468
Solution:
\(\ 468 = 2^2×3^2×13 \)
⸫ The number 468 is to be divided by 13 so that it becomes a perfect square.
(ii) 1584
Solution:
\(\ 1584 = 2^2××2^2×3^2×11 \)
⸫ The number 1584 is to be divided by 11 so that it becomes a perfect square.
(iii) 2645
Solution:
\(\ 2645 = 5×23^2 \)
⸫ The number 2645 is to be divided by 5 so that it becomes a perfect square.
7. In a military camp the major has to arrange 1764 soldiers in a square shape such that the number of soldiers along the length and the breadth are equal. How manty soldiers are there in each row?
Solution:
On factorising the number of soldiers, we have
⸫ \(\ \sqrt{1764} = 2×3×7 = 42 \)
⸫ There are 42 soldiers in each row.
8. Find the smallest perfect square number which is divisivle by 4, 9 and 10.
Solution:
The smallest number which is divisible by 4, 9 and 10 is the LCM of the numbers 4, 9 and 10
So, LCM \(\ (4,9,10) = 2^2×3^2×5 = 4×9×5 = 180 \)
But the number 180 is not a perfect square, for making it a perfect square number, let us factorise it as follows,
It is observed that 5 occurs single in RHS of the above equation. So, multiplying the equation by 5 we can make 180 a perfect square number.
180×5 = 900
⸫ 900 is the smallest perfect square number which is divisivle by 4, 9 and 10.
9. Find the square root by division process:
(i) 2116
Solution:
(ii) 4761
Solution:
(iii) 576
Solution:
(iv) 6084
Solution:
10. Find the square root of the following decimal numbers.
(i) 12.25
Solution:
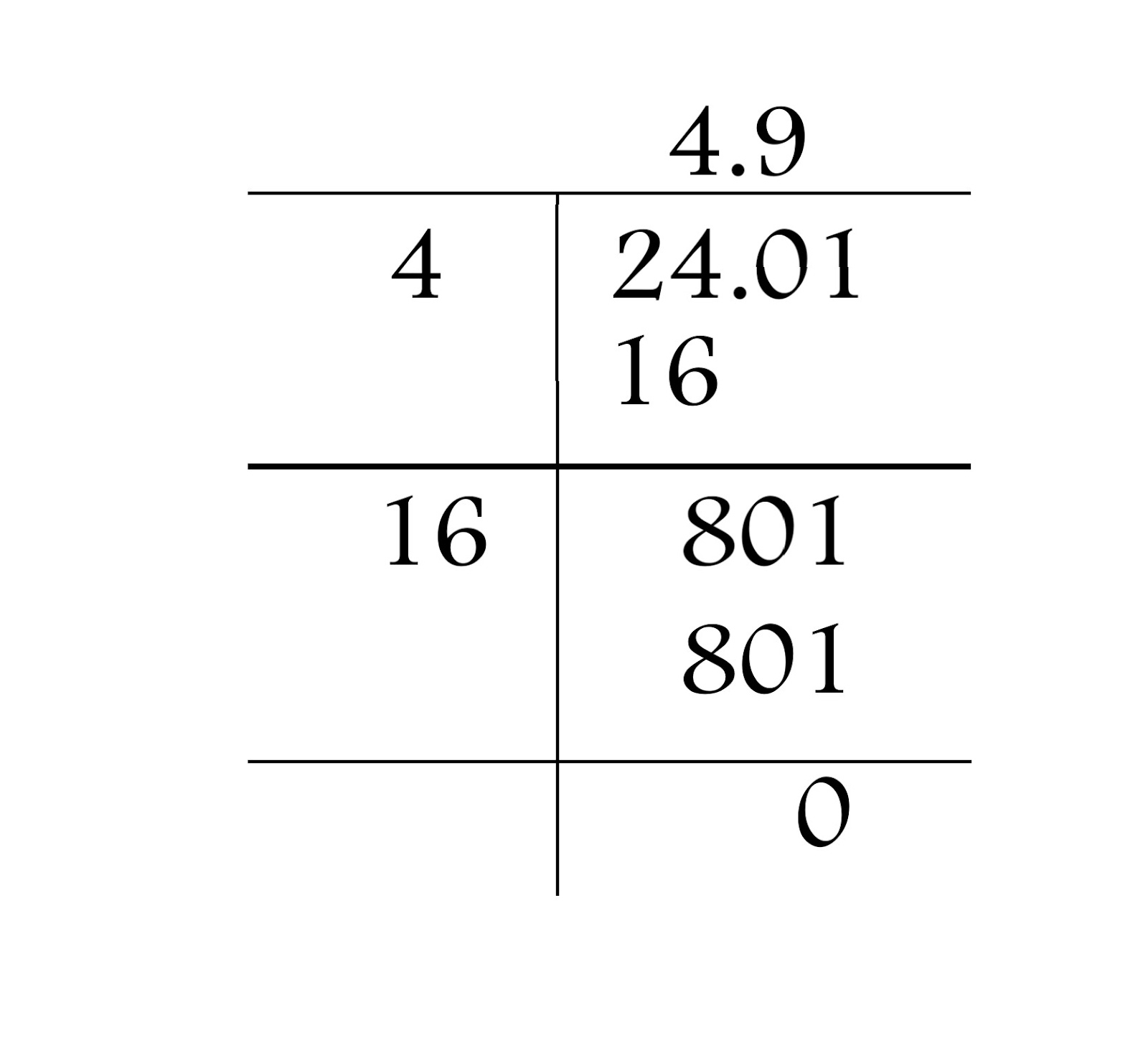
(ii) 24.01
Solution:
(iii) 146.41
Solution:
(iv) 102.01
Solution:
11. Find the correct option:
(a) Which of the following is a square of an odd natural number?
(i) 256
(ii) 169
(iii) 546
(iv) 754
Solution: (ii) 169
Explanation: The square of an odd number is again an odd number.
(b) Which of the following will have 1 (one) in the unit place?
(i) \(\ 19^2 \)
(ii) \(\ 34^2 \)
(iii) \(\ 18^2 \)
(iv) \(\ 20^2 \)
Solution: (i) \(\ 19^2 \)
Explanation: Since \(\ (9)^2 = 81 \)
i.e., 1 in unit place.
(c) Between \(\ 18^2 \) and \(\ 19^2 \) how many natural numbers are there?
(i) 38
(ii) 36
(iii) 42
(iv) 40
Solution: (ii) 36
Explanation: For two consecutive perfect square numbers \(\ n \) and \(\ n+1 \), there are \(\ 2n \) natural numbers.
If \(\ n = 18 \) then \(\ n+1=18+1=19 \) and therefore, \(\ 2×18=36 \)
(d) Which of the following is not a perfect square?
(i) 441
(ii) 572
(iii) 576
(iv) 729
Solution: (ii) 572
Explanation: The numbers having the digits 2,3,7 and 8 in their unit places can't be perfect squares.
(e) If \(\ \sqrt{2025} = 45 \) then \(\ \sqrt{20.25} \) is equal to
(i) 45
(ii) 4.5
(iii) 0.45
(iv) 0.045
Solution: (ii) 4.5
Post a Comment